Design of a Nanometre-Precision Air Gap Control for Planar Magnetic Bearing Actuators
 Ralf Volkert, Mirko Büchsenschütz, Thomas Sattel
Ralf Volkert, Mirko Büchsenschütz, Thomas Sattel
Ilmenau University of Technology
Mechatronics Laboratory, Ilmenau, Germany
Reprinted with Permission
Abstract
Planar magnetic bearings for multi-coordinate drives with high-precision positioning capabilities often consist of several electromagnetic actuators, using reluctance forces which levitate a movable platform in six degrees of freedom. This paper shows a test bench structure for individual testing of a single actuator. Two different test procedures focus on the identification of force characteristics and the examination of active control performance. A practical approach of PI state space controller design is given for a planar magnetic bearing actuator and then verified by measurements. The presented procedure is suitable to several types of position controlled electromagnets and not limited to magnetic bearing applications.
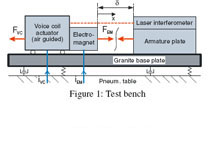
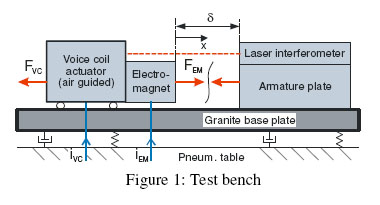
1 Test bench
At the test bench (Fig. 1) the electromagnet is attached to the air-guided slider of a voice coil actuator. A translational motion is only possible in one horizontal direction (x). A flat armature plate for the electromagnet is fixed to the granite base. The adjustable force FVC generated by the voice coil actuator pulls the electromagnet away from the armature plate, whereas the force FEM of the electromagnet counteracts. By supplying the electromagnet coil with the current iEM, the air gap d between electromagnet and armature plate can be controlled. The slider displacement is measured by a laser interferometer with a resolution of 0.08 nm. All control algorithms have been tested on dSPACE hardware with a sample rate of 10 kHz.
2 Plant identificiation
The relation between reluctance force FEM, the current iEM and air gap length d is nonlinear. It has been precisely measured on the test bench shown in Fig. 1. A PI position controller adjusts the slider at a constant air gap length d. As the force constant is known, the current iVC of the voice coil indicates the acting force FVC. By increasing current iEM the reluctance force of the electromagnet is increased. The PI position controller regulates iVC and thereby FVC to keep the desired position. At standstill, there are only two forces acting on the slider in opposing directions and the same amount. FEM equals FVC and iEM is known. Automated multiple measurements within the operation range of 100…900 μm result in the characteristic curve FEM (iEM, d).
Besides the nonlinear static behaviour, the plant also consists of time-linear elements, which are related to the slider (GS,mech(s)) and the transfer function of the power electronics (GS,el(s)) that controls the current iVC (1).
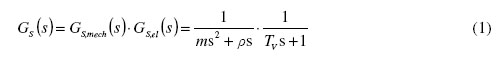
The mechanical parameters consist of the slider mass m and the damping factor ρ that have both been identified by an oscillation experiment including a spring with known spring constant that is fixed to the slider mass and the armature plate. The test procedure includes excitation of the spring, sudden release and measurement of the frequency of oscillation and the decay curve of the oscillation amplitude to get m = 7.92 kg and ρ = 7.9 Ns/m. The electrical time constant Tv = 8×10 -5 s approximates the measured frequency response of the current regulator within the current source (power amplifier).
3 Air gap control structure
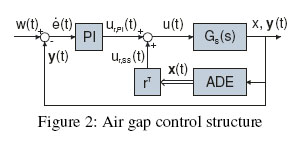
The presented controller is an enhancement of the PIDD² controller presented in [1]. The whole control structure consists of a linear PI state space controller and the inverse characteristic curve of the nonlinear part of the plant. This structure allows to freely choose all zeros and poles of the closed loop system. The state vector x(t) of the linear PI state space controller includes the slider’s position x, the velocity x& and the acceleration &x& . As only x is directly measured, the missing components of x(t) are calculated by a noise suppressing algebraic derivative estimation algorithm (ADE) [2]. The output vector y(t) includes only the position x. The actuating variable u(t) is the scalar force value FEM that is converted to the corresponding electric current using the inverse nonlinear characteristic curve iEM(FEM, d). As the inverse nonlinear characteristic curve and the forward nonlinear behaviour of the plant compensate each other, a consideration of the force generating current iEM is not necessary for the dynamic aspects in control design. Fig. 2 shows a schematic of the resulting top-level control structure. The next section shows the pole placement procedure of the complete closed loop system.
4 Parameter selection for the PI state space controller
The first step to determine all amplification parameters is to convert the system model into the time domain in matrix notation (2,3).
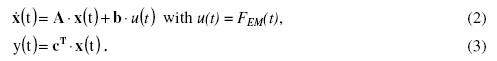
The actuating variable u(t) consists of the state feedback ur,SS(t) and the output of the PI controller ur,PI(t) (4).
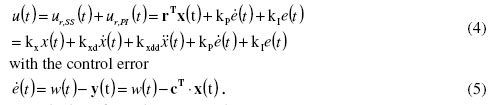
To calculate the poles of the closed loop system including the PI controller, it is necessary to extend the state vector x(t) by the integrated control error e(t). With w(t) = 0 the resulting extended state space formulation is as follows.
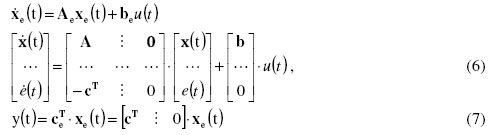
With (4) and (6) we get the complete equation of the PI state space controller (8) where (7) is still the output equation.

The state space formulation can be written as the control transfer function:

GCTF(s) has one zero placed at n1 = -110 and four poles that have been placed as follows: p1 = -15000, p2 = -160, p3 = -100, p4 = -30. The corresponding parameters in GCTF(s) were gained by equating the coefficients. In theory it is possible to freely determine the dynamic capabilities of the system, practically they are mainly limited by saturation current and noise level of the amplifier.
The poles can be freely chosen to ensure good system dynamics with practically applicable parameters. The robustness is supported by the top-level PI controller [3].
References
[1] Volkert, R.; Sattel, T.; Bertram., T.: Reduction of Disturbance Effects and Positioning Noise for High-Precision Planar Magnetic Guidances. EUSPEN 9th international conference 2009, San Sebastian, Spain, Proceedings Vol. 1, 374-377. [2] Zehetner, J.; Reger, J.; Horn, M.: A Derivative Estimation Toolbox based on Algebraic Methods – Theory and Practice. IEEE 2007 Multi-conference on Systems and Control (MSC 2007). Singapore, 2007. [3] Lutz, H., Wendt., W.: Taschenbuch der Regelungstechnik, 6., erweiterte Auflage. Wissenschaftlicher Verlag Harri Deutsch, Frankfurt am Main, 2005.Contact us today for a complimentary consultation

