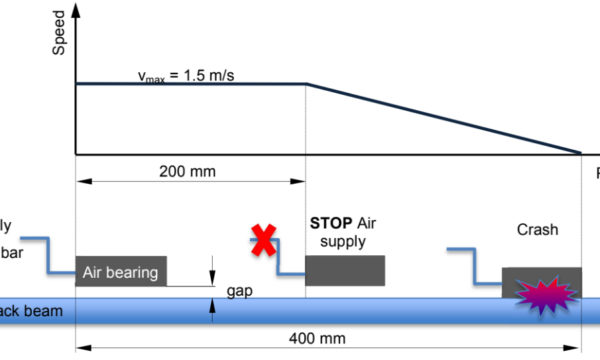
New Way Air Bearings ® has always been at the forefront of porous media air bearing technology. This extends to fostering and supporting the research literature which underpins air bearings as an area of study for modern innovation.
Much has been written about exact solutions for the kinematics and performance of cylindrical Porous Gas Bearings (PGB’s), but in the paper Porous Gas Journal Bearings: An Exact Solution Revisited and Force Coefficients for Stable Rotordynamic Performance, by Luis San Andres, Jing Yang and Andrew Devitt and published in the MDPI Journal of Applied Sciences, the authors revisit historical models and develop a new exact solution; comparing its results to high fidelity Finite Element (FE) models for predicting the performance of New Way manufactured PGB’s.
The full paper is enclosed in this link to provide you with the full mathematical analysis on the kinematics and exact modeling of cylindrical PGB operation. However, this technical paper will hone in on the primary points of interest and conclusions drawn from the work of Andres, Yang and our founder, Drew Devitt.
Boundary Conditions
Going back to the 1970’s, traditional modelling of PGB’s heavily relied upon numerical analysis which disregarded flow physics, dimensional analysis, and otherwise operated upon assumptions of inviscid flow and velocity potential, rather than considering the truer physicality of viscous flows with nonzero slip and shear conditions.
Beginning by establishing boundary conditions for PGB operation, we see their performance is determined by geometry (radial density c, length L and Diameter D0, relevant gas physical properties, supply pressure, air pressure, porous media permeability (k), liner radial thickness t, shaft angular speed 𝛀 and processional frequency 𝝎. The pressure field, under the influence of non-zero slip conditions (accounting for viscous effects) is given by:
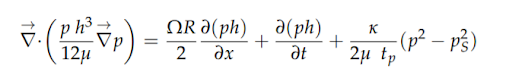
Producing a periodic result, while the mass flow rate is given by:
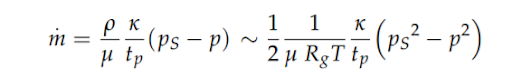
These boundary conditions and governing equations combine to produce 3 dimensionalized quantities which define operational parameters, given by:
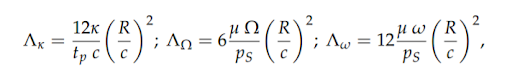
Which are known as the flow feeding number, the speed number and the frequency number, respectively. For a rotating shaft, aerodynamics effects (given by Λk ) dominate over aerostatics effects while squeeze film effects dominate for Λw > 1.
Important Notes From the Historical Literature
Research into the kinematic operation, analysis and modelling of PGB’s began in the 1960’s, and only began to mature in the 1980’s. Analytical solutions were derived under assumed aerostatic conditions. This provided reasonable results at the time, but the solutions no longer mesh with the heavily aerodynamic applications of the modern porous media gas bearing, as their usage has expanded into the power generation and rotary motion sectors.
Furthermore, many original authors did not study the effects of frequency (which constitutes an oversight for the modern era, given turbomachinery applications), and damping coefficients weren’t studied at all. Early analysis also did not account for the volume of the porous material, which if thick enough can induce a pneumatic hammer effect not dissimilar from poorly tuned orifice air bearings.
Later analysis in 1979 would determine that in hybrid operations (with rotational motion), stiffness and damping are cross coupled, providing one of the profound benefits of the porous media product. In a companion study, they also identified the positive relationship between supply pressure and bearing centering stiffness (the porous air bearing’s self centering tendency makes them an ideal for rotary applications). At Texas A&M University, San Andres and his lab have helped to determine the stable responses of porous gas bearings under rotordynamic condition, revealing their subsynchronous whirl frequencies and their unusually high damping ratio (above 10%).
Closed Form Solutions
One of the most substantial results of this research was the development of first- and zero-order equations for pressure fields, shown below.
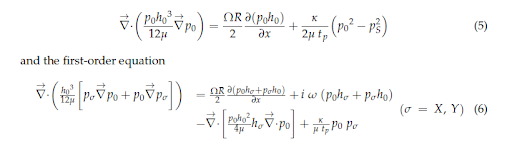
Applied over the flow domain, pressure fields allow for an analytical solution to force, torque, drag, power, and dynamic coefficients. This provides the foundation of a comprehensive Finite Element model of a PGB. It also leads to the understanding that mass flow through the bearing is almost entirely a function of bearing geometry, pressure differential, and permeability, rather than any viscous effects which may arise due to rotation.
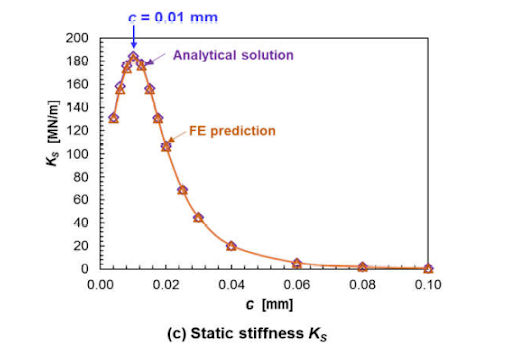
For engineers interested in aerostatic operation of bearings (like shaft bearings operating along a linear axis), this research also quantified the static stiffness coefficients, equation 32 in the text.
Figure 4c in the original text shows us the correlation between clearance and static stiffness. More importantly, it demonstrates the strong agreement between the Finite Element model which underpins the work, and the raw analytical solutions.
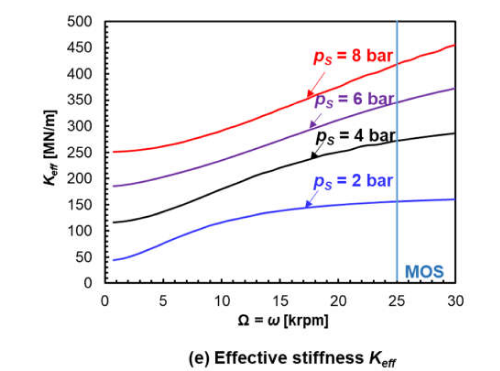
The work continues with the analysis of PGB force coefficients as a function of rotor speed, demonstrating comprehensively a positive correlation between load capacity and rotational speed (see figure 6e below).
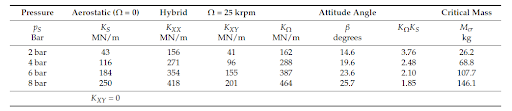
For turbomachinery applications, higher pressure and higher angular velocity opens the door to larger scale applications, especially with the modular nature of air bearing technology (further reading on the applicability of air bearings to turbomachinery may be found here). This also leads into an examination of stability and instability, giving us a threshold for the critical mass of a point mass rotor simply supported on a PGB. The work may be seen fully derived in the text, and the results are shown below in this table:
These analytical solutions and FE models also capably model the usage of PGB’s for off center, (i.e. eccentric) masses, and reveals that load increases linearly with the eccentricity ratio, as shown below:
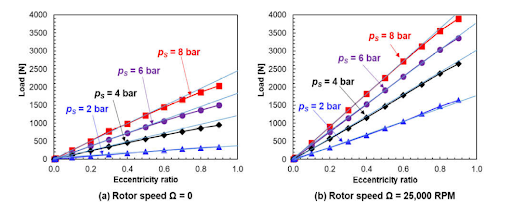
Of particular interest is the exceptional agreement between the finite element model and the exact solution, helping to further validate the methods defined in this paper.
Concluding Remarks
The work contained herein by Andres, Yang and our own Drew Devitt represents a remarkable leap forward for a mathematical understanding of porous gas bearing operation, analysis and simulation. While we would highly recommend reading the source material in it’s comprehensive entirety, we hope this technical overview provides you with an appreciation for the level of fidelity with which modern porous media bearings are understood, and the degree of confidence you can have in their ability to support your next project.
To learn more about the practical applications of porous media air bearings for industries, download our ebook, Overcome the Challenges Facing the Medical Industry with Air Bearings.
If you have any questions or wish to consult with our dedicated engineering staff, please contact us.